Pixelgrafiken mit Portable Anymap

Ein besonders einfaches Grafikformat ist Portable Bitmap. Dieses wird zwar im Alltag kaum benutzt, ist aber durch den einfachen Aufbau leicht zu verstehen und funktioniert prinzipiell wie alle anderen Formate auch.

Aufgabe 2

• Lies den wikipedia-Artikel über Portable Bitmap: http://de.wikipedia.org/wiki/Portable_Bitmap
• Analysiere die Datei hallo.pbm Hilfe eines Text- und eines Binär/Hex-Editors. Was zeigt die Grafik? Überprüfe mit Hilfe eines Grafikprogramms wie Irfan View oder Gimp.
• Erzeuge mit einem Binär- oder Hex-Editor eine Datei initialen.pbm, die Deine Initialen zeigt. Es soll die Binärversion des Formats benutzt werden. Die Breite des Bildes sollte durch 8 teilbar sein (Ansonsten müssen angefangene Bytes in einer Zeile z.B. mit 0 aufgefüllt werden). Teste deine Datei mit einem Grafik-Programm wie z.B. Irfan View oder Gimp.
• Erkläre die Größe der Datei.
• Beurteile die Bedeutung der ASCII-Version des Formats.

Aufgabe 3

• Analysiere die Datei graubild.pgm und erkläre das Zustandekommen des Bildes, das Du in einem Grafikprogramm sehen kannst.
• Erstelle selbst ein Bild mit Hilfe eines Binär-/Hexeditors.
• Erkläre die Größe der Datei.

Aufgabe 4

• Analysiere die Datei farbbild.ppm und erkläre das Zustandekommen des Bildes, das Du in einem Grafikprogramm sehen kannst. Die letzte Zeile des Bildes musst Du nicht genau erklären können, da es sich um Punkte beliebiger Beispielfarben handeln soll.
• Erstelle selbst ein Bild mit Hilfe eines Binär-/Hexeditors.
• Erkläre die Größe der Datei.

Kompression von Daten

Vergleicht man die Dateigröße z.B. Bildern einer Digitalkamera mit der Größe, die man rechnerisch erwarten würde, stellt man fest, dass diese erheblich voneinander abweichen. Die Daten der Digitalkamera müssen also komprimiert sein. Dabei gibt es prinzipiell unterschiedliche Möglichkeiten der Datenkompression.

Aufgabe 5

1. Erstelle ein farbiges (RGB) Bild mit Gimp der Größe 100 x 100 Pixel, in das Du z.B. ein paar Punkte o.ä. einzeichnest. Welche Größe wird das gespeicherte Bild voraussichtlich belegen? Begründe mathematisch.
2. Speichere das Bild in den Formaten png (Kompressionsgrad 0), png (Kompressionsgrad 9) und jpg (niedrigste Qualität) ab. Vergleiche die Bilder mit einem Hexeditor (nur oberflächlich) bzgl. Inhalt und mit einem Bildbetrachter bzgl. Qualität und Größe der Dateien.
3. Lies den einführenden Abschnitt unter http://de.wikipedia.org/wiki/Datenkompression und erkläre die auftretenden Effekte. Benutze dabei die Begriffe "verlustfrei" und "verlustbehaftet". Nenne dabei auch weitere Beispiele aus dem Computerbereich und aus dem sonstigen Alltag.

Huffman-Codierung

Eine Möglichkeit Daten verlustfrei zu komprimieren stellt der Huffman-Code dar.Dieses Verfahren wird z.B. -in Kombination mit anderen Verfahren- bei PNG-Grafiken oder ZIP-Dateien benutzt.

Aufgabe 6

1. Beschreibe je anhand eines Beispiels für UTF-8 und Morsen, wie Information mit Hilfe unterschiedlich langer Codierungen dargestellt werden kann. Beschreibe die Grundidee dieser Codierungen.
2. Mit Hilfe der Huffman-Codierung können beliebige Daten komprimiert werden, bspw. auch Texte oder Bilder. Dazu wird ein Binärbaum benutzt. Ein Beispielbild der Größe 5x3 Pixel ist im folgenden dargestellt:
   
   1. Erkläre die Beschriftung der Knoten und Kanten des dazugehörigen Binärbaums möglichst allgemeingültig.
      
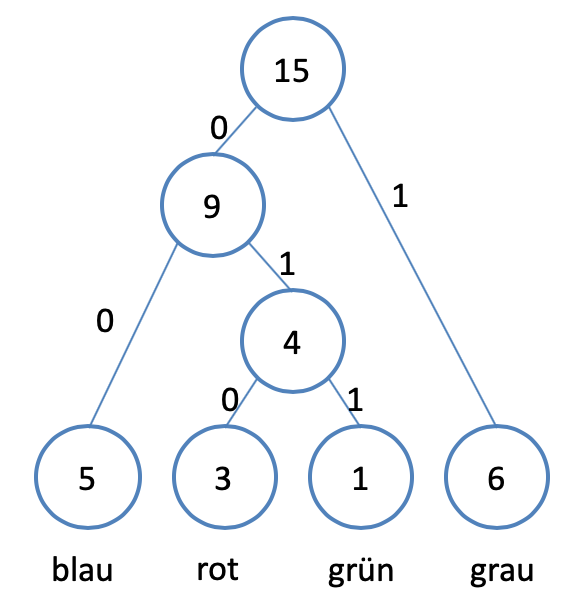
   2. Die Codierung dieses Bildes lautet 1110110101110001000000000010. Erkläre den Zusammenhang zwischen Bild und dessen Code. (Tipp: Der Zusammenhang wird am deutlichsten, wenn Du den Code Pixel für Pixel in drei Zeilen darstellst.)
   3. Wie groß wäre das Bild, wenn man es unkomprimiert im RGB-Modell speichert (Bei je 256 möglichen Werten für Rot, Grün, Blau)? Vergleiche mit der Größe der komprimierten Datei und erkläre den Unterschied.
3. Stelle Dir Deine Umgebung als Foto vor. Weshalb kann dieses Foto nicht mit obigem Baum codiert werden? Welche Konsequenz ergibt sich daraus für das Speichern einer komprimierten Datei und deren Inhalt.
4. Im ungünstigsten Fall kann eine komprimierte Datei geringfügig größer sein, als eine unkomprimierte. Begründe.

Erzeugung eines Huffman-Baums

Mit Hilfe des Huffman-Codes lassen sich beliebige Daten komprimieren. Oft wird die Funktionsweise anhand von Texten erklärt, weil das Verfahren hier gut verständlich ist.

Aufgabe 7 - Kompression von Text

1. Experimentiere mit einer Simulation z.B. anhand des Wortes "HANNA" und eines komplexeren Beispiels. Beschreibe stichwortartig wie ein Huffman-Baum erstellt wird.
2. Erzeuge per Hand (auf Papier) den Huffman-Baum für ein selbst gewähltes Wort oder einen kurzen Satz und codiere den Text.

Im Prinzip funktioniert die Kompression bei Bildern mit dem Huffman-Code genauso.

Aufgabe 8 - Kompression von Bildern

1. Formuliere den Algorithmus um, so dass er auf Bilder anwendbar ist.
2. Zeichne ein Beispielbild der Größe 5*3 Pixel, das mehrere Farben enthält.
3. Erstelle einen passenden Binärbaum für Dein Bild.
4. Codiere das Bild mit Hilfe des erstellten Baumes
5. Vergleiche den Speicherplatzbedarf nach der Kompression mit dem Speicherplatzbedarf ohne Kompression. (Lege bei der Speicherung ohne Kompression das RGB-System mit 8Bit pro Farbe zu Grunde. Vernachlässige die zu speichernde Informationen über Größe des Bildes etc.)

http://www.inf.fh-flensburg.de/lang/algorithmen/code/huffman/huffman.htm

Verlustbehaftete Kompression

Durch Huffman-Codierung lassen sich Daten verlustfrei komprimieren, da dabei keine Informationen verloren gehen. Oft nimmt man bei der Kompression einen Verlust von Informationen in Kauf. Dann spricht man von verlustbehafteter Kompression. Dies wird z.B. bei dem weit verbreiteten JPG-Format angewendet.

Aufgabe 9

Speichere ein Bild in verschiedenen Qualitätsstufen im jpg-Format ab. Beschreibe die auftretenden Effekte.